Sección de raíces cuadradas

Extracción rápida de las raíces

Intenta calcular tarea siguiente en la mente:
Quadratwurzel aus 75076 = ?

El extraer una raíz es tarea de cálculo compleja. Sólo muy pocas personas pueden resolverlo sin una calculadora. El maestro contador de cabeza lo hace en la cabeza.

Cuando alguien habla de extraer la raíz se supone la raíz cuadrada. Así que la segunda raíz se llama una raíz cuadrada. La raíz es una potencia invertida. Si tomamos la 2. potencia de 9, eso es 9 subido al 2 o también 9*9 = 81. Entonces, si queremos extraer la raíz de 81 es de nuevo el 9 Esta es la segunda potencia o la raíz cuadrada. Aquí una vista general de potencias de 1-32.

Si nos fijamos en los resultados se puede ver que la potencia de 1 y 9 siempre termina con 1. La potencia de 2 & 8 siempre 4, la potencia de 3 & 7 siempre 9 y todavía la potencia de 4 & 6 siempre Finaliza 6. La potencia de 5 a 5, y la de x0 a 0. Esto es importante para el procedimiento posterior.

En la escuela hemos aprendido a extraer la raíz así:

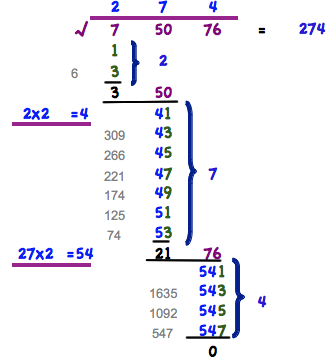
• 1. Número a la izquierda repartido en grupos de dos
• 2. Ahora resta de los números impares del grupo de izquierda. Comienza con 1, hasta que un residuo positivo sigue ahí! Así que 7-1 = 6, 6-3 = 3, 3-5 = - 2 ya no funciona ..
• 3. Contar el número de números impares. Esta es la primera cifra de la solución (2).
• 4. Al residuo (3) añadir el siguiente grupo de a 2 (50). El número 350 es el resultado.
• 4. Multiplicar el resultado actual por 2 (2x2 = 4). Esta es la nueva base a la cual se suman los números impares (4x) y restan del valor de (350)
• 6. Proceda como se describe en 2. 350-41 = 309, 309-43 = 266, 266-45 .....
• 7.Proceder al igual que descrito en 3. - 5. 3. cantidad de números impares (7), 2. cifra de la solución. 4. añadir próximo grupo de a 2 (2176), 5. multiplicar resultado por 2 (27x2 = 54)
• 8. Proceder como descrito desde 4. A el resto (21) y el siguiente bloque de 2 (76), resulta en (2176). 2176-541 = 1635, 1635-543 = 1092, ...

Los pasos desde la 5. puedes repetir hasta que el resultado es suficientemente preciso o el resto es 0.

Otro método para resolver la raíz cuadrada.

Para esto necesitas las potencias del principio del artículo.

En nuestro ejemplo la raíz cuadrada de 75076

Dividimos el 75.076 en 2 bloques. 750 & 76

Así termina la potencia en 76 Este poder es de 4 y 6, ya que siempre termina en las 6

Ahora estamos buscando la mayor potencia posible para no exceder el 750. Esta es la 27. Debido a que 27x27 = 729

Entonces, la solución puede ser sólo 27 4 o 27 6.

Nosotros utilizamos un truco y tomamos la potencia que se encuentra en el medio y termina en la 5. Así que la potencia de 275.

Potencias de cinco son relativamente fáciles de calcular. Para ello, dividimos los 275 en 27 & 5 Luego tomamos el 5x5 = 25 y 27x27+1 = 27x28. Ese es la potencia de 27 = 729x27=756 Ahora se combinan los dos resultados -75625

Ahora la prueba, está la buscada raíz (75076) debajo de la potencia de xx5 (75625), es la baja de las dos posibles potencias, está por encima, es la otra

Por lo tanto la buscada es inferior a la 5. potencia, así es 274 la correcta.

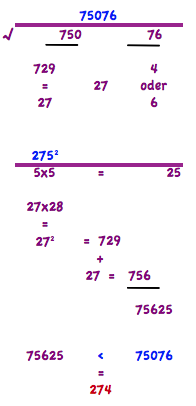
Supongamos para ilustrar todavía un ejemplo diferente. Estamos en busca de la raíz de la 12769. Esto se traduce en 2 bloques 127 y 69 Así acaba en 9. Posibles potencias con 3 ó 9. La mayor potencia no es mayor que 127 es el 11. Por lo tanto, los candidatos posibles 11 3 & 11 9. Ahora, la potencia de 115. 11x11 = 12.1+11 = 132. 132 & 25 = 13225. De nuevo, esto es sobre el buscado 12769, por lo que debajo de los dos candidatos. La raíz 12769 =113

Así va todo en la cabeza:

Da ich keine vernünftige Anleitung zum ziehen einer Quadradwurzel gefunden habe warte ich auf eine Anleitung von einem Kopfrechensportler.

Instrucciones: Sacar raíces cuadradas - Calcular raíces cuadradas

Memoria a largo plazo es un almacén permanente de conocimientos. Almacena todas las impresiones, experiencias, información, emociones, habilidades, palabras, fechas y hechos que se han acumulado a lo largo de nuestras vidas. Esto hace el conocimiento general de una persona. A diferencia de Kurzzeitgedächtnis su capacidad es prácticamente ilimitada. La información puede almacenarse en la memoria a largo plazo de minutos a años o incluso toda la vida.

Memoria a largo plazo es, ya que el psicólogo canadiense Endel Tulving 1972 publicó sus estudios, dividido en dos grupos principales: la memoria declarativa (también llamada memoria de conocimiento) y la memoria procedimental (también llamado comportamiento de la memoria).

La memoria declarativa / memoria de conocimiento