Dyscyplina - pierwiastek

Szybkie pierwiastkowanie

Spróbuj w pamięci obliczyć, ile wynosi:
Quadratwurzel aus 75076 = ?

Pierwiastkowanie jest skomplikowanym zadaniem. Nieliczne osoby potrafią sobie z tym poradzić nie używając kalkulatora. Mistrzowie liczenia w pamięci potrafią sobie z tym poradzić bez kalkulatora.

Jeśli ktoś mówi o pierwsiastkowaniu, to ma zazwyczaj na myśli pierwiastek kwadratowy. Czyli drugi pierwiastek to pierwiastek kwadratowy. Pierwiastkowanie jest odwrotnością potęgi. I tak na przykład 9 do potęgi 2 oznacza 9*9 = 81. Pierwiastek drugiej potęgi z 81 to 9. Poniżej zestawienie potęg od 1 do 32.

Przyglądając się wynikom można stwierdzić, że potęga liczb 1 i 9 kończy się zawsze liczbą 1. Potęga 2 & 8 zawsze liczbą 4, potęga 3 & 7 zawsze liczbą 9 a potęga 4 & 6 zawsze liczbą 6. Potęga liczb 5 kończy się liczbą 5, a potęga x0 liczbą 0. To ważna informacja na przyszłość.

W szkole tak nas uczono pierwiastkowania:

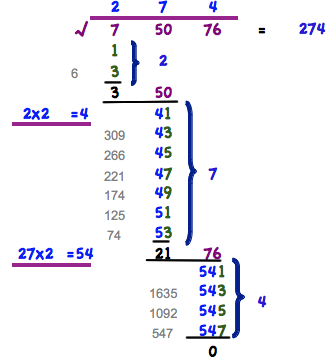
• 1. Podzielić liczbę na grupy dwójkowe po lewej stronie.
• 2. Z grupy po lewej stronie odjąć liczby nieparzyste. Rozpocząć od 1 i kontynuować tak długo, jak długo wynik pozostaje dodatni! A więc dla przykładu: 7-1=6, 6-3=3, natomiast działanie typu 3-5= - 2 nie jest już możliwe.
• 3. Zliczyć ilość liczb nieparzystych. W ten sposób otrzymujemy 1. cyfrę rozwiązania (2).
• 4. Do reszty (3) dodać następną grupę dwójek (50). W ten sposób otrzymujemy wynik 350.
• 5. Dotychczasowy wynik należy pomnożyć przez 2 (2x2=4). Do tak powstałej podstawy dołączymy liczby nieparzyste (4x) i odejmiemy od wartości (350).
• 6. Dalej postępować tak, jak podano w punkcie 2. 350-41=309, 309-43=266, 266-45…
• 7. Dalej postępować tak, jak podano w punktach 3- 5. Czyli: 3. Zliczyć ilość liczb nieparzystych (7), 2. Cyfra rozwiązania 4. Dołączyć następną grupę dwójek (2176), 5. Wynik pomnożyć przez 2 (27x2 = 54).
• 8. Dalej postępować tak, jak podano od punktu 4. Reszta (21) i następny blok dwójek (76) tworzy kombinację (2176). 2176-541=1635, 1635-543=1092…

Kroki opisane od punktu 5 możesz powtarzać tak długo, jak długo wynik jest wystarczająco dokładny lub gdy reszta równa jest 0.

Innym sposobem na pierwiastkowanie jest sposób opisany poniżej:

W tym celu będziesz potrzebował(a) potęgi z początku artykułu.

Według naszego przykładu będzie to pierwiastek z liczby 75076.

Liczbę 75076 dzielimy na dwa bloki: 750 & 76.

Potęga kończy się liczbą 76. Do dyspozycji mamy wynik 4 & 6, ponieważ wynik ich potęgowania zawsze kończy się liczbą 6.

Teraz musimy odnaleźć możliwie największą potęgę, która nie jest większa od 750. To może być tylko 27, ponieważ 27x27=729.

Rozwiązaniem może być albo 27 4 albo 27 6.

Posłużymy się pewną sztuczką i wybierzemy potęgę, która znajduje się gdzieś pomiędzy i kończy się liczbą 5. Czyli chodzi o potęgę z 275.

Potęgi z 5 można obliczyć stosunkowo szybko. W tym celu należy podzielić 275 na 27 & 5. Następnie mnożymy 5x5 = 25 oraz 27 x 27+1 = 27x28. Czyli chodzi o potęgę z 27= 729+27= 756. Teraz trzeba tylko połączyć obydwa wyniki i otrzymujemy 75625.

Zadaniem było odszukanie pierwiastka (75076) poniżej potęgi xx5 (75625). Musimy wybrać spośród dwóch możliwych potęg.

Szukany pierwiastek jest mniejszy od potęgi xx5, czyli prawidłowym rozwiązaniem jest liczba 274.

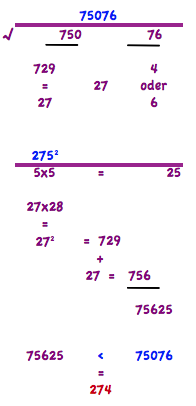
Dla lepszego zrozumienia posłużmy się innym przykładem. Szukamy pierwiastka z 12769. Liczbę dzielimy na 2 bloki 127 & 69. Ostatnią liczbą jest 9. W grę wchodzą liczby 3 lub 9. Największą potęgą, która jest mniejsza niż 127, jest 11. Możliwymi kandydatami są 11 3 & 11 9. Teraz potęga z 115. 11x11 = 121+ 11= 132. 132 & 25= 13225. Wynik leży powyżej szukanej liczby 12769, czyli musimy wybrać liczbę mniejszą od podanych kandydatów. Pierwiastek 12769 = 113.

A tak można to obliczyć w pamięci:

Ponieważ nie udało mi się do tej pory znaleźć rozsądnej wskazówki odnośnie pierwiastkowania, zdecydowałem się poczekać na radę mistrza liczenia w pamięci.

Wskazówka: Pierwiastkowanie – obliczanie pierwiastka kwadratowego

Chodzi o obliczenie w pamięci pierwiastka z liczby 5-cyfrowej. Przy odrobinie wprawy na pewno sobie z tym poradzisz. W jaki sposób szybko nauczysz się tej umiejętności, znajdziesz w rozdziale Sposób na pierwiastkowanie.

W miarę usprawniania swoich umiejętności, będziesz ćwiczył(a) na coraz wyższym poziomie.

Tutaj wprowadzenie do poziomu: