Szybkie mnożenie
Spróbuj w pamięci obliczyć, ile wynosi:
319 x 546 = ?
Mnożenie liczb jednocyfrowych jest stosunkowo proste. Liczenie 1x1 przerabialiśmy w szkole. Z takim mnożeniem jesteśmy sobie w stanie poradzić bez problemu w pamięci. Mnożenie liczb 2-cyfrowych jest wprawdzie trudniejsze, ale i z nim poradzimy sobie. Chodzi tu o mnożenie od 1x1 do 20x20. Powyżej tej granicy nasza umiejętność liczenia w pamięci napotyka na poważne trudności. Wtedy jesteśmy skazani na liczenie na kartce papieru.
W szkole tak nasz uczono mnożenia na kartce:
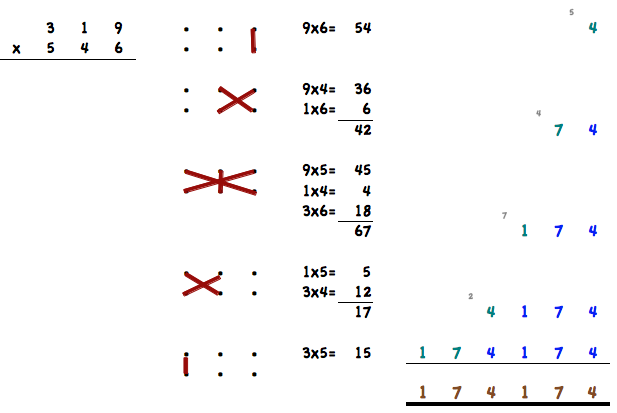
Zaczynamy mnożyć z prawej strony liczby 6x9 = 54. 4 notujemy poniżej w pierwszej linijce, a 5 zapamiętujemy. Następnie mnożymy 6x1=6 plus 5 z pamięci daje 11. 1 wpisujemy poniżej w pierwszej linijce po lewej, obok 4. Następnie 6x3=18 + 1 z pamięci = 19. Teraz robimy to samo z liczbą 4 od 546. Czyli 4x9=36. 6 wpisujemy na dole pod 4 do drugiej linijki a 3 przenosimy. I tak dalej. To bardzo wiele kroków, za wiele na mnożenie w pamięci.
Czy jest sposób na mnożenie w pamięci?
Metodę, którą stosują mistrzowie liczenia w pamięci, nazywa się wedyjskim mnożeniem. Ten sposób liczenia pochodzi z Indii i sprawia, że liczenie w pamięci staje się proste. Wyjaśnię na przykładzie, na czym polega ta metoda.
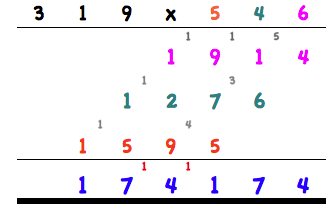
Metoda ta nazywana jest również metodą krzyżową. Grafika wyjaśnia, dlaczego. Najpierw pomnożymy pierwsze cyfry z prawej strony. 9x6=54. 4 można zapisać na dole jako rozwiązanie. 5 zapisać w pamięci. Następny krok to pomnożyć obie ostatnie litery na skrzyż. 9x4=36 oraz 1x6=6. Razem daje to 42 + 5 z pamięci = 47. 7 zapisać na dole jako rozwiązanie a 4 zapisać w pamięci. Trzeci krok to mnożenie wszystkich cyfr na skrzyż. 9x5=45, 1x4=4, 3x6=18, razem 67 + 4 z pamięci = 71. 1 zapisać na dole jako rozwiązanie, 2 zapisać w pamięci. Ostatni krok to mnożenie dwóch cyfr po prawej stronie. 3x5=15, +2 z pamięci = 17. Zanotować. Wielką zaletą tego systemu jest to, że rozwiązanie możesz od razu zapisać z prawej do lewej. W ten sposób oszczędzamy na czasie, bo rozwiązania pośrednie, tak jak to miało miejsce w liczeniu na kartce papieru, nie jest już konieczne.
Podczas rozgrywek mistrzowskich do jednej z konkurencji należy mnożenie liczb 2-cyfrowych.

Jak zapewne już zauważyłeś(aś), również i tutaj obowiązuje ta sama zasada, jak podczas mnożenia 3x3. Z prawej do lewej i zawsze na skrzyż. Na sam początek proponuję Ci ćwiczenia 2x2, następnie 3x3. Po opanowaniu tej metody, możesz spróbować liczenia w pamięci 5x5. Również i tu obowiązuje ta sama zasada: ćwiczyć, ćwiczyć, ćwiczyć. Opłaca się. Podczas liczenia w pamięci aktywowanych jest jednocześnie kilka obszarów mózgu. To bardzo skuteczny trening mózgu!
Wskazówka: Mnożenie
W zadaniu tym chodzi o jak najszybsze mnożenie w pamięci liczb 3-cyfrowych. Zadanie to należy wykonać w miarę szybko i bezbłędnie. Przy odrobinie cierpliwości oraz ćwiczeń z pewnością sobie poradzisz. W jaki sposób możesz nauczyć się szybkiego mnożenia, zostało opisane w rozdziale Metoda mnożenia.
A tutaj przykład:
| 832 | |
| x | 678 |
Teraz musisz obliczyć, ile to wyniesie. Jeżeli zadanie zostało prawidłowo rozwiązane, to wynik brzmi 564.096. Aby nie stracić orientacji, ospowiednia informacja została wyświetlona w tabeli.
W miarę usprawniania swoich umiejętności, będziesz ćwiczył(a) na coraz wyższym poziomie.
Tutaj wprowadzenie do poziomu:
| Level | + 5 minut | Dodatek | × 5 cyfr | Dodatek | × 8 cyfr | Dodatek | √ 5 minut | Dodatek |
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| 2 | 2 | 0 | 2 | 0 | 2 | 0 | 2 | 0 |
| 3 | 3 | 0 | 3 | 0 | 3 | 0 | 3 | 0 |
| 4 | 4 | 0 | 6 | 0 | 4 | 0 | 4 | 0 |
| 5 | 5 | 0 | 9 | 0 | 5 | 0 | 5 | 0 |
| 6 | 6 | 0 | 12 | 0 | 6 | 0 | 6 | 0 |
| 7 | 6 | 1 | 12 | 3 | 6 | 1 | 6 | 1 |
| 8 | 7 | 1 | 15 | 3 | 7 | 1 | 7 | 1 |
| 9 | 8 | 1 | 18 | 3 | 8 | 1 | 8 | 2 |
| 10 | 9 | 1 | 21 | 3 | 9 | 1 | 10 | 2 |
| 11 | 10 | 1 | 24 | 3 | 10 | 1 | 12 | 2 |
| 12 | 11 | 1 | 27 | 3 | 11 | 1 | 14 | 2 |
| 13 | 12 | 1 | 30 | 3 | 12 | 1 | 16 | 2 |
| 14 | 12 | 2 | 30 | 6 | 12 | 2 | 16 | 4 |
| 15 | 13 | 2 | 33 | 6 | 13 | 2 | 18 | 4 |
| 16 | 14 | 2 | 36 | 6 | 14 | 2 | 20 | 4 |
| 17 | 15 | 2 | 39 | 6 | 15 | 2 | 22 | 4 |
| 18 | 16 | 2 | 42 | 6 | 16 | 2 | 24 | 4 |
| 19 | 17 | 2 | 45 | 6 | 17 | 2 | 26 | 4 |
| 20 | 20 | 0 | 54 | 0 | 20 | 0 | 32 | 0 |
 Menü
Menü
