Disciplina koren

Hitro korenjenje

Poskusi rešiti naslednjo nalogo na pamet:
Quadratwurzel aus 75076 = ?

Računanje korena je kompleksna računska operacija. Le redki jo zmorejo brez kalkulatorja. Mojstri v računaju na pamet pa jo izvajajo kar "iz glave".

Ko govorimo o korenu, mislimo običajno na kvadratni koren. Koren je obrnjena potenca. Če vzamemo drugo potenco na 9, je to 9 na kvadrat ali 9 * 9 = 81. Če sedaj korenimo 81, dobimo znova 9. Govorimo o korenu iz 81. Oglej si potence 1-32.

Če podrobno pogledaš rezultate, vidiš, da se potenca 1 in 9 vedno konča z 1. Potenca števil 2 in 8 se vedno konča s 4, potenca števil 3 in 7 z 9, potenca števil 4 in 6 pa vedno s 6. Potenca števila 5 se konča s 5, tista od x0 pa z 0. To je sedaj pomembno za nadaljnji postopek.

V šoli smo se korenjenje učili tako:

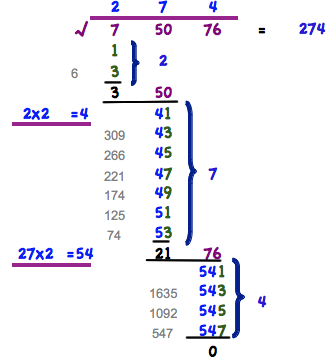
• 1. Razdeli število proti levi v skupini po dve
• 2. Odvzami iz leve skupine liha števila. Začni z 1, dokler še imaš pozitiven ostanek. Torej 7-1=6, 6-3=3, 3-5=-2 pa več ne gre.
• 3. Preštej število lihih števil. To je 1. število rešitve (2).
• 4. Dodaj k ostanku (3) drugo skupino dveh števil (50) - dobimo število 350.
• 5. Pomnoži dosedanji rezultat z 2 (2x2=4). To je nov temelj, na katerega bomo pripeli liha števila (4x) in jo odšteli od nove vrednosti (350)
• 6. Postopajmo kot opisano pri 2. 350-41=309, 309-43=266, 266-45…..
• 7. Wie bei 3.- 5. beschrieben vorgehen. 3. Anzahl ungerader Zahlen (7), 2. Ziffer der Lösung. 4. Nächste 2er-Gruppe dazu (2176), 5. Ergebnis mit mal 2 (27x2 = 54)
• 8. Wie ab 4. beschrieben vorgehen. Rest (21) und nächster 2-er Block (76), ergibt (2176). 2176-541=1635, 1635-543=1092,…

Korake od 5. naprej lahko tako dolgo ponavljaš, dokler ne dobiš točnega rezultata ali da je ostanek enak 0.

Druga možnost reševanja:

Za to rabiš potence z začetka sestavka.

Naš primer korena iz 75076

Wir teilen die 75076 in 2 Blöcke. 750 & 76

Also endet die Potenz auf 76. Daraus ergibt Potenz von 4 & 6, weil diese immer auf 6 Enden

Poišči zdaj največjo možno potenco, ki ne presega 750. To je 27. 27 x 27 = 729

Rešitev je lahko samo 27 4 ali 27 6.

Poslužili se bomo trika in vzeli potenco, ki leži vmes in se konča s 5. Torej potenco iz 276.

Potenzen mit fünf sind relativ leicht zu berechnen. Hierzu teilen wir die 275 in 27 & 5. Dann nehmen wir die 5x5 = 25 und die 27 x 27+1 = 27x28. Das ist dann die Potenz aus 27= 729+27= 756. Nun die beiden Ergebnisse verbinden - 75625

Preverimo: če iskan koren (75076) leži pod potenco xx5 (75625), potem je nižja od obeh možnih potenc, če pa se nahaja nad njo, pa je druga.

Iskana leži pod peto potenco, torej je 274 pravilna.

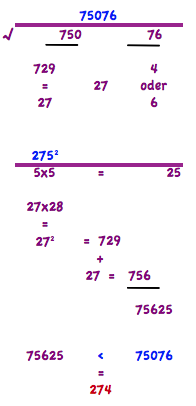
Oglejmo si še en primer. Iščemo koren števila 12769. Dobimo dva bloka, 127 in 69. Konča se torej z 9. Možni potenci sta 3 ali 9. Največja potenca, ki ne presega bloka 127, je 11. Kandidati so 11 3 in 11 9. Poglejmo potenco 115. 11x11 = 121 + 11 = 132. 132 in 25 nam data 13225. To je nad iskano 12769, torej pod obema kandidatoma. Pomeni, da je koren iz 12769 = 113.

Tako to poteka na pamet.

Da ich keine vernünftige Anleitung zum ziehen einer Quadradwurzel gefunden habe warte ich auf eine Anleitung von einem Kopfrechensportler.

Navodila: Korenjenje - izračun kvadratnega korena

Petmestno število lahko koreniš neposredno na pamet. Z nekaj vaje ti bo to gotovo uspelo. Hitro korenjenje si lahko ogledaš pri metoda korenjenja.

Boljši kot boš, višja bo tvoja raven.

Delitev ravni oz. stopenj: